HSI攻击

abstract：高光谱图像攻击中需要了解的知识
story：这篇没有story:D

A. 高光谱图像数据集

高光谱：像素的记录格式不再是rgb，而是按照光谱波段记录

Indian pine

只有一张图片，分辨率为145*145
该图片的每个像素作为一个样本，每个像素都由一个200个数字描述，表示各个波段的反射强度，理论上属于0-1
这张图拍的主要为农作物，共有16个类别，即10249个样本对应16个类别，包括草地、玉米地、林地等
Indian Pines 数据集的规模: 145*145*200 (width height 波段数)
下载得到的数据集形式
- Indian_pines.mat ：原始的Indian Pines 数据集: 145*145*220
- Indian_pines_corrected.mat 矫正后的Indian Pines 数据集: 145*145*200
- Indian_pines_gt.mat 标签矩阵 145*145

部分内容引自知乎

AVIRIS 成像光谱仪成像波长范围为 0.4-2.5μm，是在连续的 220 个波段对地物连续成像的，但是由于第 104-108，第 150-163 和第 220 个波段不能被水反射，因此，我们一般使用的是剔除了这 20 个波段后剩下的 200 个波段作为研究的对象。

145*145 = 21025=10776（背景，黑）+ 10249（多种地物，彩）
> 10249 = 各类地物占得像素个数。

解混

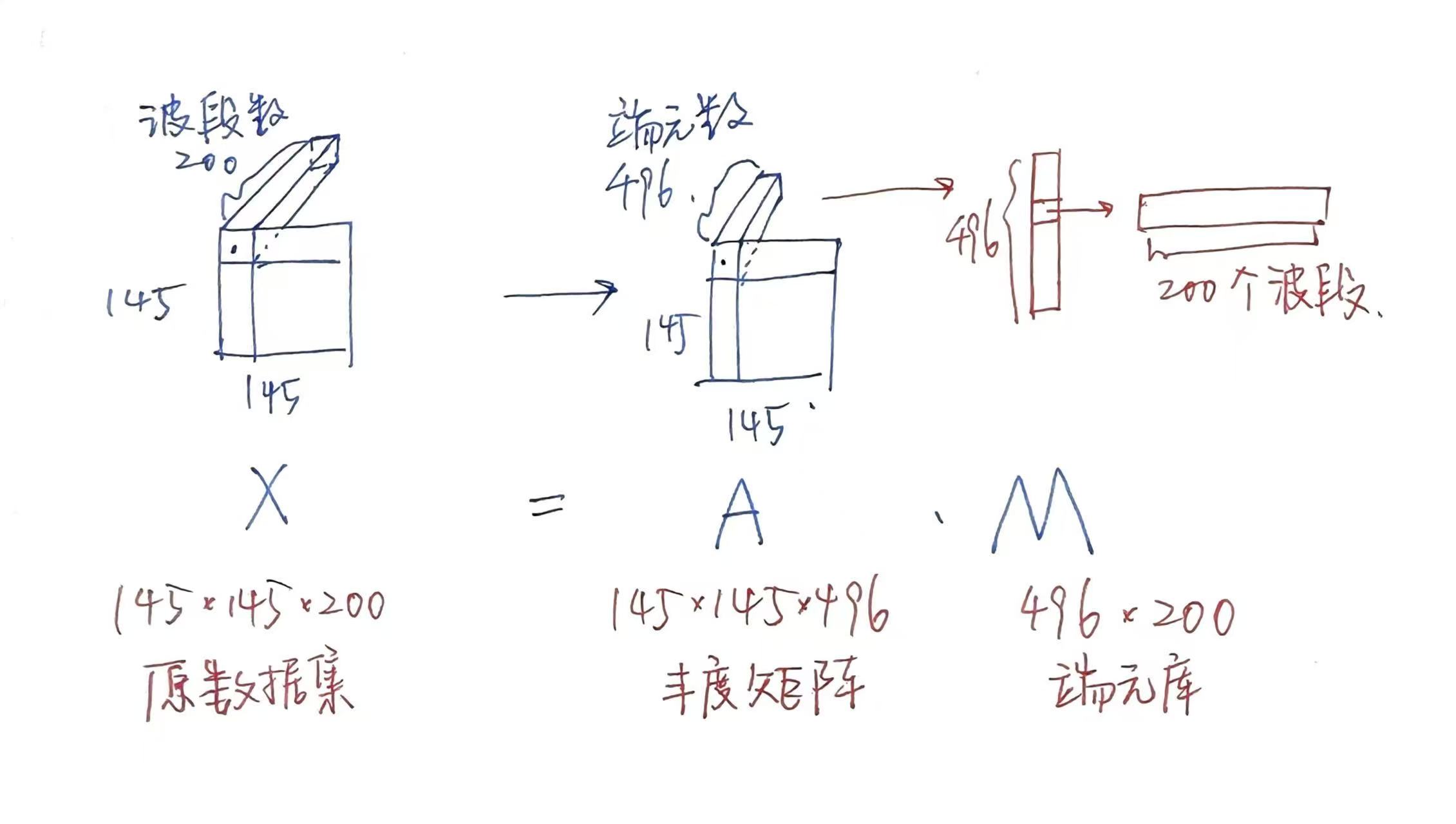
jiehun

我们对丰度矩阵A添加扰动，丰度矩阵表示每个像素中不同端元的占比，端元库表示不同端元（纯净）在光谱中200个波段下的值

B. Universal Perturbation

算法：在每一轮迭代中都找到$\Delta v$

C. 经典神经网络的训练逻辑

DataLoader

一个迭代器

pbar = tqdm(enumerate(attack_loader), total=len(attack_loader)) 
    for index, (_, abun, abun_sum, noise, labels, _) in pbar: 
    # 每次迭代使用一个batch的数据来更新扰动（正常32个，但如果最后一组样本量不足32，那就不足32，不舍弃）

用for迭代，每次迭代使用一个batch的数据来更新扰动（正常32个，但如果最后一组样本量不足32，那就不足32，不舍弃）

每个batch是一个元组，元组中有多个元素，每个元素都是一个pytorch张量，这些张量有不同的shape，而所有张量的第一维，都是batch_size。例如这里abun的形状就是$[32,6 ,15,15]$，也就是$\text{[B, C, H, W]}$
- $C$：端元数（端元要经过选择在光谱库的496个端元中筛选出整张数据集中存在的端元最终只剩6个端元【Indian_pines数据集】）
- $H、W$：高宽（输入并非一个像素，而是围绕一个像素切割出的15*15的patch，这个切割的过程有点像卷积核对图像的遍历）
每输入一个batch，也就是输入这些张量。

批量梯度下降

公式a：以batch_size=10为例

$\theta_j := \theta_j - \alpha \frac{1}{10} \sum_{k=i}^{(i+9)}(h_{\theta}(x)-y{(k)})x_j$

$\theta_j$：第$j$个参数
$\alpha$：步长
$\alpha$后面那一坨：目标函数$(h_{\theta}(x)-y{(k)})$对$x_j$ 的偏导的平均值

伪代码：

for m in epoch:
    for n in batch_num:
        for i in batch_size:
            公式a
        $\J = sum_{k}

每个epoch要完整遍历一遍数据集
数据集被划分为很多个batch，依次遍历这些batch
每个batch内部并行计算，即同时计算所有样本的预测值、损失并求平均
每算完一个batch更新一次参数：
1. 清理其他batch的梯度
2. 对之前得到的这个batch的平均损失求梯度
3. 反向传播
4. 更新参数
梯度不累计，每个batch一清理
参数累计

D. 攻击算法

sgaa

扰动逻辑

把perturb当做参数，放入传统神经网络中进行优化
逻辑同深度学习：

fsgm

扰动逻辑

perturb_i = (self.eplison*torch.sum(abun_adv.grad, dim=0).unsqueeze(0).sign()).detach() 
# 沿着丰度梯度正方向，计算扰动增量
perturb = torch.clamp(perturb+perturb_i, min=-self.eplison, max=self.eplison).detach() 
# 分离计算图，当做常数，切断上游梯度传递，切断上游参数对梯度的影响，但每次迭代，上游参数的改变会刷新这个分离出的perturb

“上游”？：
- 参数： $\mathbf{W}$ (需要梯度的参数)
- 中间计算： $\mathbf{A} = \mathbf{W} \cdot 2$
- 损失 1 (L1)： $\mathbf{L_1} = \mathbf{A} \cdot 5$
- 损失 2 (L2)： $\mathbf{L_2} = \mathbf{A} \cdot 10$
  该例子的计算图如下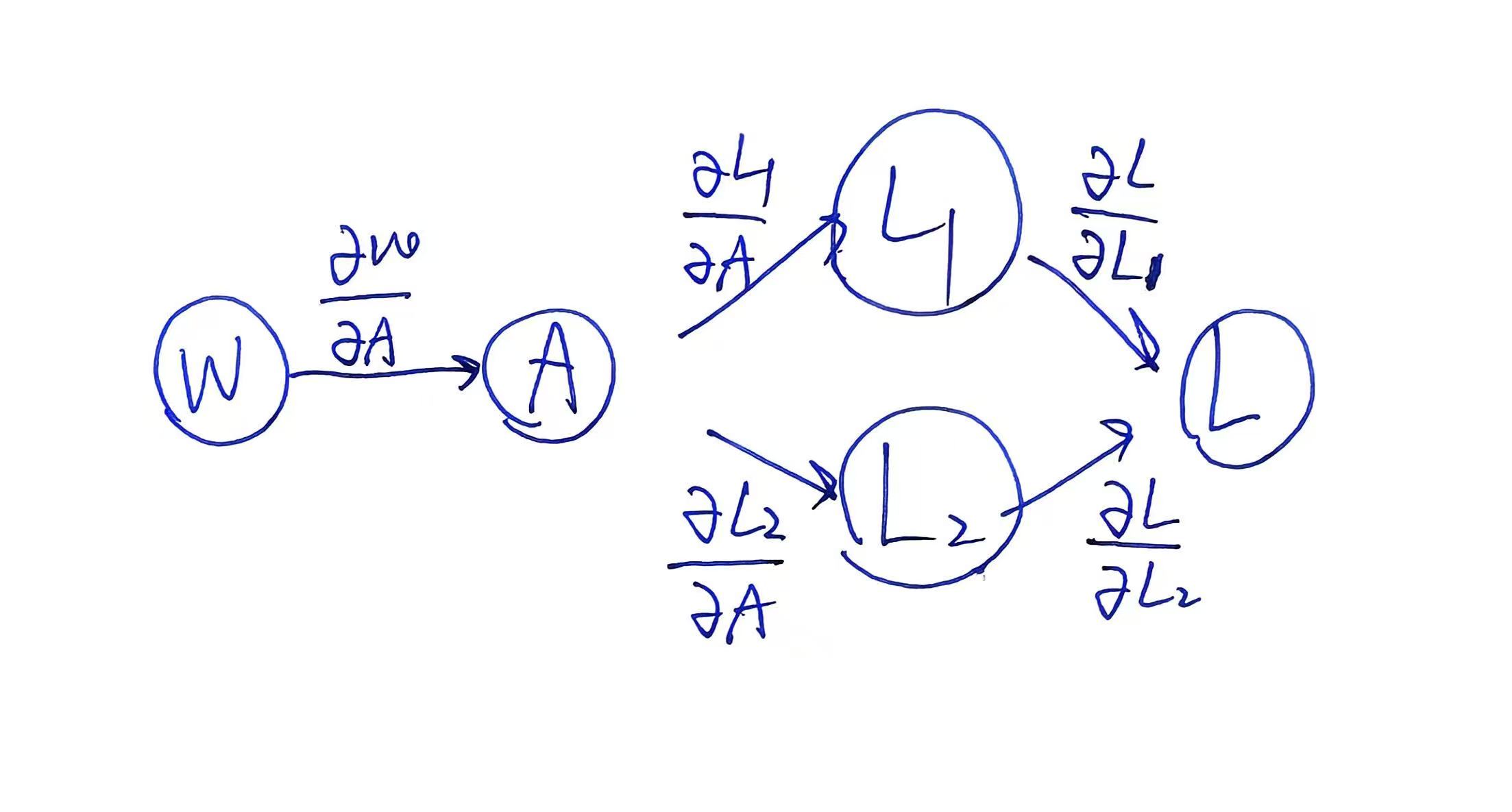
不涉及optimizer，通过分离计算图获取perturb并在每一次样本训练下更新

A. 高光谱图像数据集#

Indian pine#

解混#

B. Universal Perturbation#

C. 经典神经网络的训练逻辑#

DataLoader#

批量梯度下降#

D. 攻击算法#

sgaa#

fsgm#